Gravity
from a new angle
Mass and its unit of measurement is a
part of every day life. Gravity can be observed between two objects
with a mass. There is no effect of gravity without the presence of
mass. Modern physics, in fact all of the science is dependent on the
definition of mass and its measurement on the surface of the earth.
Recently, it even became the subject of
news when the standard mass of 1 Kg bar (International Prototype
Kilogram) kept at the International Bureau of Weights and Measures
located in the suburbs of Paris, France was reported as loosing its
mass [6] compared to its replicas kept elsewhere in the world. So, if
the mass of an object is so important in understanding the gravity and
part of every day in life, what is the mass itself?
The mass was defined around three
hundred years ago in the works of Isaac Newton and it is still being
used in the same form as depicted below.
Mass is the measure of matter in an
object. The mass of an object doesn't change if that object is heated,
bent, stretched, squeezed or compressed, or transported from one place
to another on earth or even to a position out in space.
According to the above definition, if
we compress or expand an object, the mass of the object remains same.
What is the experimental evidence for this property of the matter?
An object was never compressed or
expanded as part of an experiment to check the validity of the
definition of mass.
A smallest shape any object could attain when compressed is a point size. First, lets explore the
characteristics of this point mass object to understand more about the
mass.
Point mass object has a peculiar
position in the field of physics, with having a double definition.
Quantum mechanics and general relativity, two of the major theories in
physics, have their own definition for this point mass object and still
the concept of point mass is one of the essential part of these two
branches of physics.
According to the definition of mass,
which is mostly used in the gravitational theories rather than in
quantum mechanics, the mass of an object doesn't change even if that
object becomes a point mass.
According to the special relativity, if
the matter of an object is closely packed together, then the matter
will have more binding energy between the particles of matter.
According to the same theory, binding energy itself is mass (the
mass-energy conversion equation
E=mc2).
It means, if an object has more binding energy then that object will
measure more in mass.
So, if a group of protons and neutrons
packed together closely in a nucleus, then that nucleus will weigh more
than the nucleus in which the same set of particles occupied more space
than earlier. A closely packed or compact nucleus will have more
binding energy than the loosely packed nucleus with same number of
nucleons.
At the same time, enormous amount of
energy is required to compress a piece of one kilogram wood or iron bar
to a point size. If all the protons and neutrons in an object occupy a
point size space, then the object will have more binding energy.
According to the special relativity, more binding energy in the point
size wood means more mass it will measure. Therefore, the point size
compressed one kilogram wood will measure more mass than the normal one
kilogram wood. According to the definition of mass, both should measure
the same amount of mass. Here we see a clear conflict between the
definition of mass and the mass-energy conversion principle in regard
to the point mass object.
Among these two concepts, one is
experimentally observed and the other is a simple imagination without
any base. If we need to discard one of these two, then it would be the
definition of mass.
Similar to the compact and expanded
nucleus, if we compress an object, that object will measure more in
gravity to the earth; therefore weighs more than the normal object. If
we expand the same object, it will measure less gravity to the earth.
Therefore the mass of an object, as we measure it today, does change
with the size of the object.
What is the uniqueness in an object
that determines the amount of mass inside it? The only distinct thing
in an object is the subatomic particles it contains. Then, is the mass
of that object is the total count of the subatomic particles inside it?
According to the standard theory, the count of particles is not the
mass of the object.
Then, is the mass of an object is the
total mass of subatomic particles in it? The answer is still a no.
Combined mass of all the subatomic particles in an object will be
greater than the mass of the object. Then, what exactly is a mass of
one kilogram of iron sphere means? Apart from saying that it is equal
in comparative mass to the standard kilogram preserved at the
institute, it doesn't stands for anything the object contains according
to the standard definitions.
Weight, a similar term used along with
the mass, was defined as the gravitational force between the mass of
the object and the mass of the earth. So, by differentiating mass from
weight, it was made to believe that the mass of an object is unique and
doesn't depend on the gravity of earth on the object. In reality, both
mass and weight are dependent on the gravity of the earth.
If we balance one kilogram of iron bar
and one kilogram of loosely bound cotton in a balance scale as shown in
Fig.1, then what is common in them? Everything differs in them
including the size, shape, number of subatomic particles except the
gravity of the earth on each of these objects. When the pull of gravity
on these two objects is equal then the balance will be parallel to the
surface of the earth. So the mass, we
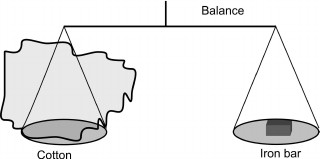
Figure 1: Cotton and iron bar in a balance scale
defined as one of the standard units,
is in fact wholly dependent on the gravity between the earth and the
object.
Therefore, there is not much difference
between the mass and weight of an object according to the present
definitions; both are dependent on the gravity of the earth on the
object.
Therefore, if a point mass object
measured more in mass means it actually measuring more gravity to the
earth. Binding energy within the object has no relation to increase in
the mass of the object. The compactness of the object is enabling in
exerting more gravity to the earth. Therefore, point mass objects exert
more gravity than their normal counterparts.
There used to be one trivia question
like which weighs more, between one kilogram of cotton and one kilogram
of iron? Let's explore the answer to this question. With the
invalidation of the point mass definition of mass, it is now evident
that the gravity differs with the size of an object. If we compress one
kilogram of loosely bound cotton to the size of one kilogram iron bar,
then the cotton weighs more than the iron bar. The difference might be
very small, but it is distinguishable. So, answer to the question is
cotton weighs more than the iron bar if we keep the size and shape of
both the objects as same. Now, can we say that the mass of the cotton
has increased? The only thing that changed in the cotton is its size.
The size of the cotton was decreased. Then, does the mass depend on the
size; can we measure the mass in cubic meters?
So the current definition of mass, as
we are using it today, is flawed and not a standard one. The mass of an
object keeps changing with multiple factors. It is not at all a measure
for the matter inside an object. It is only a measure for the
comparative gravity of the earth to the objects. But the amount of
matter inside an object, the total number of basic particles, is same
irrespective of shape and size of the object. Then how can we make the
amount of matter inside an object as a standard or fundamental unit?
Before attempting to redefine the mass as an amount of matter inside an
object, let's first explore if there is anything in the nature similar
to the mass as we are using it in our day to day activities.
In the nature, there are only particles
and the forces between them. There is nothing like mass of an object.
The strength of the force within the object is determined by how
tightly the particles, atoms and molecules are packed together. In
other words, the strength of the force is dependent on the density of
particles within an object.
We normally assume that among the same
size objects the heavier object has more mass. In fact the correct term
to use for the heavier object is that it has more density of matter.
As there is no time at an instance and
no distance at a point, for a single object there is no way to measure
the mass within the object. Mass as we measure it today is a
comparative gravity of the earth between the standard unit and the
object being measured. Because gravity changes with the size and
structure of the object, there is no way to determine the absolute
value for the mass of an object. Therefore we can't define a standard
unit for the mass to use anywhere in the universe.
We can only measure the comparative
gravity of the objects to the earth on the surface of the earth at a
given location. The strength of gravity of the earth to each of the
objects may not remain same anywhere else on the surface of the earth
or inside the earth or even away from the earth's surface.
Mass should represent an approximate
measure of the matter inside an object. To make the mass as a
measurable quantity, we need to keep both the objects being compared as
a same size and shape. If the source gravity on which the measurements
are made is very strong compared to the earth, then even the same size
and shape objects measuring equal mass on earth might weigh differently
depending upon their internal atomic structure. No two objects on earth
are of same atomic structure, means the number and the position of
subatomic particles are different in both the objects even if they are
of same size and shape. Therefore to keep the uncertainty to a minimum,
we need to define the size and shape for the standard measurement as a
sphere of smallest uniform volume among all materials. We need to take
that as a standard volume for the measurement of mass. Then we need to
measure the strength of earth's gravity at a location on each of the
material of standard volume and that will be the mass of the standard
volume object for that material. This is similar to the calculation of
density of an object with a difference being the smallest volume
instead of one centimeter cube.
Standard
mass of an object = Earth's gravity on a standard volume object at a
location.
Let’s define mass index ( Mi)
of a material, similar to the density, as the ratio between the
standard mass of the object and the standard volume.
Mass
index of a material,
Mi=
(Standard mass of an object's material) / (Standard volume) --- Eq. 1.
Now on, the measurement of total
mass inside an object will only depend upon the volume and mass index
of the object.
Total mass in an object =
(Total volume of the object) * (Mass index of the material) --- Eq. 2.
In this calculation of mass,
irrespective of the shape of the object, the mass inside an object
remains same and represents the measure of matter inside the object.
The total gravity of the earth on the object may vary depending upon
the shape of the object but the mass remains same irrespective of the
shape of the object as long as the matter with which it was made is
same. One thing to remember in this aspect is that if the size of an
object changes then it should be treated as a different material and
then a new standard mass has to be calculated for that material. For
example the standard mass for the loose cotton and the compressed
cotton has to be different as well as for water and ice.
Once the mass index for a material has
been calculated, then the mass of an object made from that material
should be calculated as the product of its volume and the mass index,
it should never be dependent on a measurement based on the gravity
again. It means, the mass of an object should never be measured in a
balance scale.
Let's suppose there are 1024 pieces
(easy number to make half till it reaches 1 in 10 steps) of a material
in object A,
with each piece having a volume of 1 cm3
and each piece measuring n
units of mass according to the new definition as shown in Fig 2. For
simplicity let’s still call the unit as a gram and the mass
of the cube as n
grams.
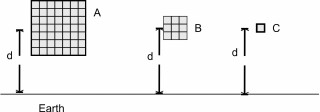
Figure 2: Change in standard mass with the size of the object
As the standard unit of measure for the
mass of a material dependent on the gravity of the earth at a location,
the weight of an object at the same location also depends upon the
gravity. At a specific location, there is no difference between the
mass and the weight of an object therefore the same unit of measure
will be used to represent the total earth's gravity on an object.
Actual gravity of object A
to the earth will measure less than (1024 * n)
grams and lets assume it as X
grams. When the object A
got compressed to half of its size to a size of 512 pieces of 1 cm3
as in object B
at the same location as object A
then the gravity of the earth on the object
B will increase and lets assume
it as Y
grams. When the object compressed, the standard mass of the object
B will also become double from
that of the object A
to (2 * n)
grams because the density of the matter in the new object got
increased. When the object A
got compressed to half of its size for 10 times to a size of 1 cm3
as in object C
at the same location, its gravity to the earth will increase further
more and lets assume it as Z
grams. Now the Z
grams is in fact equals to exactly (1024 *
n) grams. The standard mass of
the object C
will double 10 times to that of the object
A.
Z
grams = (1024 * n) grams > Y grams > X grams.
The gravity of these objects differs but all the objects are having
same amount of mass according to the new definition of mass.
Mass
= volume * mass index
If we take the 1 cm3
as the standard volume, then the standard mass will be equal to the
mass index of the material.
Mass
of A = 1024 * n grams
Mass of B = 512 * (2* n) grams
Mass of C = 1 * (1024 * n) grams.
Therefore, even though all the three
objects are having the same amount of matter, the measure of gravity
for these objects equals to the mass in an object only when that object
itself is of the size equal to the standard volume.
When the objects are bigger in size,
even if it has more matter, their gravity to the earth will be less.
When the same object compressed to a smaller size, all of its matter
concentrates at a small volume and ultimately measures more gravity.
If we measure the gravity as the
interaction between two standard volume objects then the volume can
also be a visible volume of the object. As the object's standard mass
increased as we compressed it, the same way, the standard mass of an
object will also increase as it looks smaller and smaller from the
earth. Let’s take three similar objects A,
E and
F of each 1024 cm3
made with same material and keep them at different distances from the
earth as shown in Fig 3.
Object A
measures the same amount of gravity,
X grams, as in the Fig 2. The
object E,
even though it is bigger than the object
B, it is appearing in volume
same as the object B
when viewed from a point on the earth. It means, it got visually
compressed to the size of object
B. Therefore its
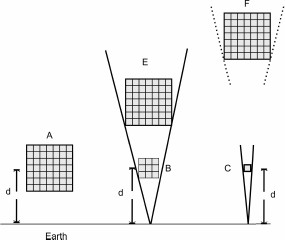
Figure 3: Change in standard mass with distance
standard mass should be measured equal
to the standard mass of the object B
as in Fig 2. In the same way, the standard mass of the object
F should be measured as (1024 *
n) grams because it is far away
and is appearing as a cube of 1 cm3
as the object C
in Fig 2. Therefore the standard mass of object
F is greater than the object
E and the standard mass of object
E is greater than that of the
object A.
So, the mass as we measure it today is
a comparative gravity and it changes with the shape and size of the
objects. Therefore the present definition of mass should not be
considered as a basic unit of measurement.
Mass of an object should be considered
as a constant irrespective of a location and that should be the product
of the volume of the object and mass index of the material of the
object.
As the standard mass of an object
increases as it compressed, the standard mass of an object will also
increase if the object appears smaller from the surface of the earth.
Earth's gravity on an object will
change when an object is compressed. Gravity will also change when
different objects regrouped as a single entity.
Scenario
1: Let's suppose a pile of loose
cotton was balanced with 100 kg of iron bar in a balance scale. Volume
of the cotton will be much bigger than the volume of the iron bar. When
the cotton is compressed to the size of the iron bar of 100 kg, the
compressed cotton bar will weigh more than the iron bar.
Scenario
2: The total weight of a pile of
sand grains will be less than the combined weight of each individual
sand grains. If we assume the weight of a single sand grain as
x
grams then the total weight of the pile of sand of one thousand grains
will be less than (1000 * x)
grams.
As the one thousand grains compress
into less volume, the weight of the pile will increase. When one
thousand grains compressed to the size of a single grain then the
weight will be equal to (1000 *
x) grams.
Weight of individual proton particle is
1.672622 x 10-24
grams. When two protons weighed together as a pile in the nucleus, the
combined weight will be less than the total of the individual protons.
This phenomenon of loss of mass in the nucleus was given a name as mass
deficit.
So, the definition of mass is flawed to
its core. It is one of the biggest mistakes in science. Scientific
community got an opportunity to correct the definition of mass when the
mass difference was observed in the radioactive decay between same
number of basic particles before and after the decay of elements.
Instead of correcting the definition of mass, scientific community
created an exception to the definition of mass and termed it as the
mass deficit. If mass, the way we defined and measure, is the
representation of matter then it should always be same for any given
object no mater what happens with the object.
Almost every principle in physics is
dependent on the definition of mass. If the definition of mass itself
is flawed then all the principles derived using the mass are also
flawed.
Date posted: October 1, 2009
Copyright
2009 Karunakar Marasakatla


